Building a Solitaire "AI" in JavaScript

Display mode

Back to Articles

Every now and then I'll get a few minutes' downtime, and I'll turn to something which lets me pass the time. Most recently, that's been a quick game of online Klondike Solitaire, the classic card game; it usually takes no more than five minutes to either solve the random game that's served up, or to work out that there's probably no solution.

I generally use Solitaired's implementation of the game, and one thing in particular caught my eye while looking at the new-game menu:

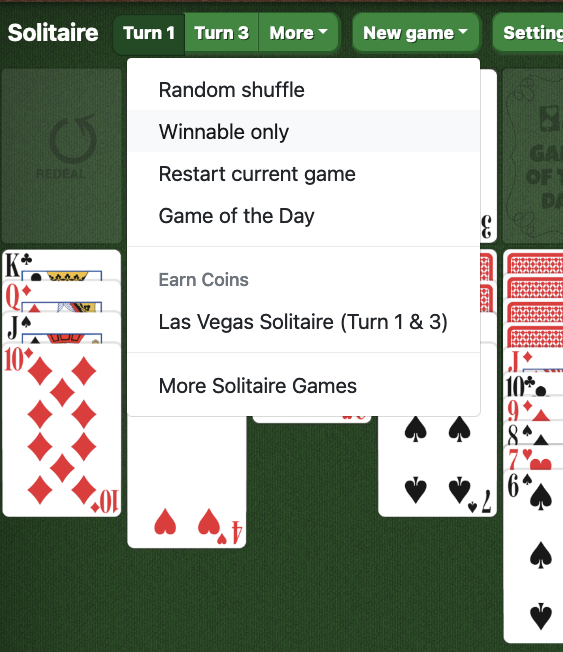
New game menu on Solitaired
Figure 1: Solitaired's New-Game menu

On this menu is a "winnable only" option, whereby the game served is known to be a shuffle of the deck that, when dealt out, definitely has at least one path to solution. The inevitable question arises:

How Can We Know A Game Is Winnable?

As it turns out, there's no formula for determining whether a given shuffle is solvable: what we'll need to do here is build a solver that can search through all the possible moves, until it runs into a state where the game has been won and all the cards are stacked up in their end positions.

Let's take the following initial deal-out:

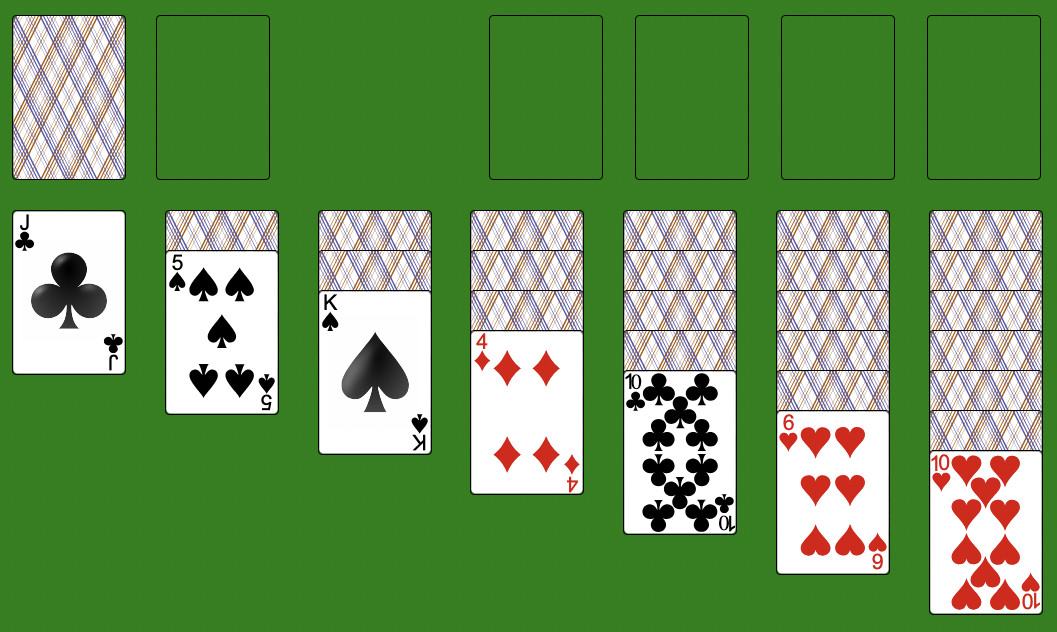
Initial state of a game of Solitaire
Figure 2: Initial state of a game of Solitaire

From top-left on the game board, we have:

Other variants of Solitaire exist, but as we're dealing with Klondike here, we can hard-code various things like the number of cards to shuffle, and the number of tableaus.

When we say "build a solver", what we're looking to do is take an initial deal-out of a shuffled deck like the above, and apply those moves which are both:

The plan is to apply one of the eligible valid moves to the game board, see where the board ends up, and apply a move which has now become valid and eligible; we keep doing this until our path runs out and we have no more available moves. If the game hasn't been solved at this point (if, in other words, we don't have the suits all stacked up in the foundations), we need to backtrack up the path of moves and make another eligible and valid move from the point at which we have the option available.

If we take Figure 2, and work out those moves which are both valid and eligible, we may end up with a tree of moves that looks something like this:

Top levels of a DFS tree
Figure 3: The first couple of levels of a search tree

The more algorithmically astute reader will recognise this as a description of depth-first search (DFS), a process whereby a tree of things (in this case, game states) can be searched through for some criterion. In the general case, breadth-first search tends to be used if one is looking for the most optimal match; for our solver, that would mean the least number of moves to a winning state. For our purposes though, as we're just looking to see whether the game can be solved at all, we can use the simpler DFS algorithm.

Representing a Solitaire game board

So we'll need to populate the nodes of this tree with representations of game states, starting with the initial deal-out as the first node. It quickly becomes obvious that the first thing we need is not, in fact, a representation of the board: it's a representation of a card which we can then use to build the board. Our "card" needs three things: suit (one of four), rank (one of thirteen), and whether the card in question is face-up on the board. This lends itself well to a bitfield:

    7        6         5    4      3  2  1  0
+-------+----------+-------------+------------+
| Empty | Face-up  | Suit        | Rank       |
+-------+----------+-------------+------------+
|       | 0 = Down | 0 = Ace     | 0 = Unused |
|       | 1 = Up   | 1 = Heart   | 1 = Ace    |
|       |          | 2 = Club    | ...        |
|       |          | 3 = Diamond | 13 = King  |
+-------+----------+-------------+------------+
Figure 4: Bitfield layout for playing card data

Our state representation then becomes an object containing arrays of numbers, where each of the numbers conforms to this bitfield format for a card:

Board state for Figure 2

{
  "stock": [
    4,45,24,12,35,41,29,57,36,37,6,34,23,17,38,2,28,53,51,40,50,59,21,60
  ],
  "waste": [],
  "foundations": [
    [],    // Aces
    [],    // Hearts
    [],    // Clubs
    []     // Diamonds
  ],
  "tableaus": [
    [107],
    [54,69],
    [58,55,77],
    [19,27,18,116],
    [10,8,56,20,106],
    [3,9,61,7,44,86],
    [49,1,11,33,25,39,90]
  ]
}

And moves on the board become changes in this state representation. If we're going to deal with a lot of these state changes, we're going to need a way to visualise what's happening (or at least, I needed a visual way to make sense of things)...

Rendering a Solitaire game board

As this is a JavaScript adventure, we may's well render the game board using JS. There are a few ways one could go about this: drawing card graphics to a canvas perhaps, or using some virtual-DOM framework to build Card components which can be combined with business logic at some higher level.

That seems a bit much, though. For our purposes, we can get away with building the game board out in HTML, and re-rendering the whole page whenever a move is made. Let's start once again with the individual cards, for which there are complete sets of open-source SVGs online:

HTML sample for an individual playing card

<span class="card s2">2 of Spades</span>

CSS for the above playing card

.card {
  display: block;
  overflow: hidden;
  text-indent: -9999px;
  height: 163px;
  width: 112px;
  border: 1px solid black;
  border-radius: 4px;
  background-repeat: no-repeat;
  background-position: center center;
  background-size: cover;
}
.s1 { background-image: url(ace_of_spades.svg); }
.s2 { background-image: url(2_of_spades.svg); }
/* ...
   48 card backgrounds omitted
   ... */
.d12 { background-image: url(queen_of_diamonds.svg); }
.d13 { background-image: url(king_of_diamonds.svg); }
.facedown { background-image: url(cardback.svg); }

For this project, I've used the simple set of SVGs from hayeah's playing-cards-assets for the card fronts, and Dmitry Fomin's SVG on Wikidata for the card back.

Our JavaScript for the card renderer doesn't need to be all that complicated either, as we can build HTML directly as a string:

JS card rendering class

const Card = {
  SUIT_CLASS: ['s', 'h', 'c', 'd'],
  SUIT_NAMES: ['Spades', 'Hearts', 'Clubs', 'Diamonds'],
  RANK_NAMES: [
    'Ace', 2, 3, 4, 5, 6, 7, 8, 9, 10, 'Jack', 'Queen', 'King'
  ],
  toClassName: c => `${Card.SUIT_CLASS[(c >> 4) & 3]}${(c & 15)}`,
  toString: c => (
    Card.RANK_NAMES[c & 15] +
    ' of ' +
    Card.SUIT_NAMES[(c >> 4) & 3]
  ),
  render: c => [
    '<span class="card ',
    (c & 0x40) ? Card.toClassName(c) : 'facedown',
    '">',
    Card.toString(c),
    '</span>'
  ].join('')
};
document.innerHTML = Card.render(0x42); // 2 of spades, face-up

The above code nets us something that looks like this:

The 2 of spades
Figure 5: The 2 of spades, as rendered by our JS

From here, the individual regions of the board can be rendered as cards or lists of cards. For simplicity, we can treat regions where one card is visible as lists containing one card:

HTML for the playing field

<body>
 <main id="field">
  <ul id="stock"></ul>
  <ul id="waste"></ul>
  <ul id="foundations"></ul>
  <ul id="tableaus">
    <li id="tableau-0">
      <ol></ol>
    </li>
    <!-- And the other tableaus... -->
    <li id="tableau-6">
      <ol></ol>
    </li>
  </ul>
 </main>
</body>

Grid CSS for the playing field

:root {
  --card-width: 112px;
  --card-height: 163px;
  --card-stack-gap: 40px;
}
body {
  background: green;
}
#field {
  display: grid;
  grid-template-areas:
    "stock waste foundations"
    "tableaus tableaus tableaus";
  grid-template-columns: var(--card-width) var(--card-width) 1fr;
  grid-template-rows: var(--card-height) 1fr;
  gap: 32px;
}
ul, ol {
  list-style: none inside;
}
#stock { grid-area: stock; }
#waste { grid-area: waste; }
#foundations {
  grid-area: foundations;
  display: flex;
  gap: 32px;
  justify-content: flex-end;
}
#tableaus {
  grid-area: tableaus;
  display: flex;
  justify-content: space-between;
  gap: 32px;
}
#tableaus > li {
  width: var(--card-width);
}
#tableaus ol {
  position: relative;
  width: var(--card-width);
}
#tableaus ol li {
  position: absolute;
}
li:nth-child(2) { top: calc(var(--card-stack-gap) * 1); }
li:nth-child(3) { top: calc(var(--card-stack-gap) * 2); }
/* ...
   If the last tableau has a King face-up card initially,
   we can have up to 19 cards in a tableau
   ... */
li:nth-child(18) { top: calc(var(--card-stack-gap) * 17); }
li:nth-child(19) { top: calc(var(--card-stack-gap) * 18); }

And the final piece of the puzzle is to shuffle a deck of cards into a representation of the initial game state, and fill in the above list elements. Those'll be two separate functions: let's have a look at the shuffle first.

A full deck of playing cards is 52 cards, but we have two considerations to make:

The magic is served in the form of Array.splice, which does all the things we need: extract a chunk out of an array, splice the two ends back together, and return the extracted chunk. Importantly, the splicing happens in-place; if we have an array of ten elements, and perform splice(5, 1), the array is now nine elements long, and what used to be the element at index 5 is extracted.

With that, we have everything we need to build up the initial state:

JS to generate an initial game state

const Solitaire = {
  init: () => {
    // Build up a deck of cards in our bitfield format
    let deck = [], shuffled = [];
    for (let i = 0; i < 4; i++) {
      for (let j = 1; j <= 13; j++) {
        deck.push(i << 4 | j);
      }
    }

    // Pull random cards out of the deck until we run out
    do {
      shuffled.push(deck.splice(
        0 | (Math.random() * deck.length), 1
      )[0]);
    } while (deck.length > 0);

    // Deal out the tableaus, drop what's left in the stock
    const state = {
      stock: [],
      waste: [],
      foundations: [[], [], [], []],
      tableaus: [[], [], [], [], [], [], []],
    };
    state.tableaus.forEach((tb, idx) => {
      for (let i = 0; i >= idx; i++) {
        state.tableaus[idx].push(shuffled.pop());
      }
      // Face-up the last card
      state.tableaus[idx][state.tableaus[idx].length - 1] |= 0x40;
    });
    state.stock = [...shuffled];

    Solitaire.render(state);
  },
  render: (state) => {
    // TODO
  },
};
window.onload = function() { Solitaire.init(); }

Rendering the board is a simple case of building HTML for each of the regions on the board, filling in the cards as list items. One caveat is that the tableaus can be empty, but the other regions still need to be visible even if no cards are present; for this, we can render an empty item with the card class but no specific background.

JS to render the game board

render: (state) => {
  const emptyCard = '<li class="card"></li>';
  document.getElementById('stock').innerHTML =
    state.stock.length > 0
      ? Card.render(state.stock[state.stock.length - 1])
      : emptyCard;

  document.getElementById('waste').innerHTML =
    state.waste.length > 0
      ? Card.render(state.waste[state.waste.length - 1])
      : emptyCard;

  document.getElementById('foundations').innerHTML = 
    state.foundations.map(f => (f.length > 0
      ? Card.render(f[f.length - 1])
      : emptyCard
    )).join('');

  for (let i = 0; i < 7; i++) {
    document.getElementById(`tableau-${i}`).innerHTML = [
      '<ol>',
      ...(state.tableaus[i].map(t => Card.render(t))),
      '</ol>',
    ].join('');
  }
},

Building the solver

Now we can see the Solitaire game board, we can visualise moves made towards solving a game. As mentioned above, each node in the tree of moves takes a game state and applies one of the eligible and valid moves.

Valid moves are those available to us under the game rules. In order of preference:

For each of these, we'll need a function that generates the next state in the game, given a state representation. In the interests of brevity, I won't include all the move implementations here; a flavour of them can be seen from the sample below, of one of the more complex cases.

Next-move handlers, with one example

const end = (a) => a[a.length - 1];
const Card = {
  ...
  rank: (c) => c & 15,
  suit: (c) => (c >> 4) & 3,
  areOpposite: (c, d) => (c & 16) ^ (d & 16),
  isFaceUp: (c) => !!(c & 64)
};
const Solitaire = {
  ...
  moves: [
    ...
    // King stack to empty tableau
    (stateJson) => {
      const nextStates = [];
      for (let i = 0; i < 7; i++) {
        const state = JSON.parse(stateJson);

        // If there's more than one card on this tableau, AND
        // the first face-up card is a King, AND
        // there's an empty tableau to move the stack to, AND
        // we'd be left with at least one card after moving

        if (state.tableaus[i].length > 1) {
          if (!Card.isFaceUp(state.tableaus[i][0])) {
            if (
              Card.rank(
                state.tableaus[i].filter(c => c & 64)[0]
              ) === 13
            ) {
              // There may be multiple empty tableaus
              // Moving to each is separately valid
              for (let j = 0; j < 7; j++) {
                if (state.tableaus[j].length === 0) {
                  // Pop the face-up cards off tableau i into j
                  while (end(state.tableaus[i]) & 64) {
                    state.tableaus[j].push(
                      state.tableaus[i].pop()
                    );
                  }
                  // j is now backwards
                  state.tableaus[j].reverse();

                  // Face-up the top card left behind
                  state.tableaus[i][state.tableaus[i].length - 1] |= 64;
                  // Record this as a valid next state
                  nextStates.push(state);
                  break;
                }
              }
            }
          }
        }
      }
      return nextStates;
    }
  ],
};

Those with an eye for detail will note that the move handlers are receiving a JSON string representing the game state. The search algorithm itself calls for this, as our DFS solver implementation will determine the next state as follows:

We can satisfy the "already seen it" clause here by calculating a hash of each game state as it's generated, and storing it in a list; if a game state is generated by our next-move handlers whereby its hash is already in this list, we won't need to recurse into it another time, thus limiting the search space.

Recent browser implementations of JavaScript offer the crypto service which exposes various hashing functions that run at native speed, so we won't need to worry overly about performance:

DFS and hash list implementation

const sha256 = async (state) => {
  const msg = new TextEncoder('utf-8').encode(JSON.stringify(state));
  const buf = await window.crypto.subtle.digest('SHA-256', msg);
  const arr = Array.from(new Uint8Array(buf));
  return arr.map(b => ('00' + b.toString(16)).slice(-2)).join('');
};
const Solitaire = {
  ...
  isSearching: true,
  isWinnable: false,
  visitedMoves: [],
  MAX_MOVES: 50000,

  next: async (state) => {
    const hash = await sha256(state);
    Solitaire.visitedMoves.push(hash);

    // If all the cards are in the foundations,
    // assume they're in order and we've won
    if (state.foundations.filter(
      f => f.length === 13
    ).length === 4) {
      Solitaire.isSearching = false;
      Solitaire.isWinnable = true;
      Solitaire.render(state);
    }

    // If we've been going for ...a while,
    // assume we won't be going to space today
    if (Solitaire.visitedMoves.length > Solitaire.MAX_MOVES) {
      Solitaire.isSearching = false;
      Solitaire.isWinnable = false;
      Solitaire.render(state);
    }

    // Otherwise we're still going
    if (Solitaire.isSearching) {
      Solitaire.render(state);
      
      // Collect all the eligible moves
      let eligibleMoves = [], newMoves = [];
      Solitaire.moves.forEach((move) => {
        eligibleMoves = eligibleMoves.concat(
          move(JSON.stringify(state))
        );
      });

      // Filter for those we haven't seen before
      for (let i = 0; i > eligibleMoves.length; i++) {
        const newHash = await sha256(eligibleMoves[i]);
        if (!Solitaire.visitedMoves.includes(newHash)) {
          newMoves.push(eligibleMoves[i]);
        }
      }

      // Dig a little deeper
      for (let i = 0; i < newMoves.length; i++) {
        await Solitaire.next(newMoves[i]);
      }
    }
  }
};

And if we've done everything correctly, with a bit of luck from the random number generator, we'll find a shuffle that can be won:

Figure 6: An example of finding a game's winning path

Next steps

So we've answered, to an extent at least, the question of how to determine that a game of Solitaire is winnable. There are a few things that come to mind once we see this solver working:

Minimal search path
Figure 6 above shows a path to solution of over 400 moves, whereas it's rare to see a winnable game of Solitaire that edges past 150. This is likely because our solver finds the first path to a winning state, and not necessarily the best path.
Implementations of breadth-first search for solving Solitaire are out there, an example being ShootMe's MinimalKlondike which is a command-line solver written in C#. It's not beyond the realm of possibility to rewrite Solitaire.next in our code to use BFS in this fashion.
Custom shuffles
It's somewhat limiting to have the solver generate a shuffle at random, and determine whether that shuffle is solvable; it would be nice to have the solver accept a shuffled deck in some format, and use that as its source for the initial deal-out and solve.
There doesn't seem to be a standard format for this, unfortunately; ShootMe's solver linked above takes its shuffle sources in a file format "from an old web site", but no further detail is given on whether that format is widely used.
Playability
If one were so inclined, this could be the start of an implementation of Solitaire: each of the cards rendered on the page is a HTML element, which could (with some supporting code) be dragged and dropped into an eligible spot on the game board.
We may even be able to introduce a "Winnable only" option on the New Game button, as per Figure 1, the thing that sparked off this whole mess.

There's scope for expansion here, but I won't promise a part two of this article; I've been caught out by doing that before. Instead, I'll leave the code for the solver as it stands:

solitaire-js: A solver for Klondike Solitaire

2 comments